ARIMA时间序列模型水质预测应用

ARIMA 时间序列模型简介

时间序列是研究数据随时间变化而变化的一种算法，是一种预测性分析算法。它的基本出发点就是事物发展都有连续性，按照它本身固有的规律进行。ARIMA(p,d,q)模型全称为差分自回归移动平均模型 (Autoregressive Integrated Moving Average Model,简记 ARIMA). 是比较成熟且简单的时间预测模型之一。其中 AR 为自回归, I 为差分, MA 为移动平均。
趋势参数：

  • p：趋势自回归阶数。
  • d：趋势差分阶数。
  • q：趋势移动平均阶数。

差分

差分（difference）又名差分函数或差分运算，差分的结果反映了离散量之间的一种变化，是研究离散数学的一种工具。它将原函数f(x) 映射到f(x+a)-f(x+b) 。差分运算，相应于微分运算，是微积分中重要的一个概念。总而言之，差分对应离散，微分对应连续。差分又分为前向差分、向后差分及中心差分三种。
通常情况下我们用到的是前向差分公式如下：
xk=x0+kh,(k=0,1,…,n)
△f(xk)=f(xk+1)−f(xk)
差分的阶
称为阶的差分，即前向阶差分 ，如果数学运用根据数学归纳法，有其中，为二项式系数。特别的，有前向差分有时候也称作数列的二项式变换

在高锰酸盐指数序列预测可行性的说明

通过观察水质变化趋势，高锰酸盐指数波动不剧烈，存在明显的中心波动规律。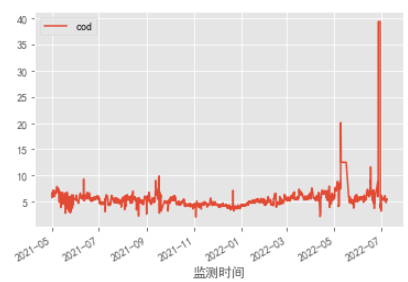

python实现

环境准备

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import warnings
import pymysql

warnings.filterwarnings("ignore")  
# 忽略警告，不然一大堆警告，多是python及对应包升高导致，不影响使用
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
from matplotlib.pylab import style  # 自定义图表风格
style.use('ggplot')

# 解决中文乱码问题
plt.rcParams['font.sans-serif'] = ['Simhei']
# 解决坐标轴刻度负号乱码
plt.rcParams['axes.unicode_minus'] = False

# pip install statsmodels

from statsmodels.graphics.tsaplots import plot_acf, plot_pacf  # 自相关图、偏自相关图
from statsmodels.tsa.stattools import adfuller as ADF  # 平稳性检验
from statsmodels.stats.diagnostic import acorr_ljungbox  # 白噪声检验
import statsmodels.api as sm  # D-W检验,一阶自相关检验
from statsmodels.graphics.api import qqplot  # 画QQ图,检验一组数据是否服从正态分布
from statsmodels.tsa.arima.model import ARIMA

连接数据

通过数据库，excel 都可以，列名为监测时间、设备名称、设备因子、监测值。

1
2
3
4
5
6
7
8
9
10
11
def conn_sql():
    conn = pymysql.connect(host=" ",
                   port= ,
                   user=" ",
                   password=" ",
                   db=" ",
                   charset="utf8")
    sql = ""
    read_sql = pd.read_sql(sql, conn)
    return read_sql
read_sql=conn_sql()

数据处理

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def nseri(s,y ):
    aidunqiao = read_sql.loc[read_sql['设备名称'] == s, :]
    ai_cod = aidunqiao.loc[read_sql['监测因子'] == y, :]
    ai_cod_mn = ai_cod.loc[:, ["监测时间", '监测值']]
    baseline = ai_cod.loc[:, ["监测时间", '监测值']]

    ai_cod_mn.set_index('监测时间', inplace=True)
    interp_cod_mn = ai_cod_mn["监测值"].interpolate()
    ai_cod_mn["cod"] = interp_cod_mn
    starttime = baseline.iloc[0, 0]
    rows = baseline.shape[0]
    endtime = baseline.iloc[rows - 1, 0]

    year_month_day = pd.date_range(starttime, endtime, freq="h").strftime("%Y%m%d%h%m%s")
    a_ser = pd.DataFrame({'监测时间': year_month_day})
    a_ser.set_index('监测时间', inplace=True)
    df = pd.concat([a_ser, ai_cod_mn], axis=0, join="outer")
    df = df.reset_index(drop=False)
    df['监测时间'] = pd.to_datetime(df['监测时间'])
    df1 = df.drop_duplicates(subset="监测时间", keep="last", ignore_index=True)
    df2 = df1.sort_values(by="监测时间", ignore_index=True)
    df2["cod"] = df2["监测值"].interpolate()
    df2.drop(columns="监测值", inplace=True)
    df2.set_index('监测时间', inplace=True)
    return df2

主要是 将数据生成无空连续的逐小时 时间序列数据 插值方法为线性插值

数据解读

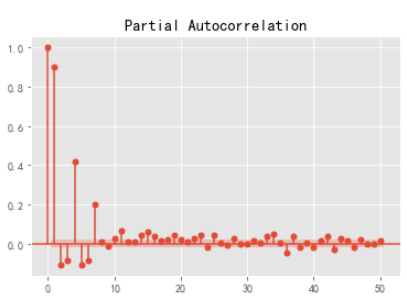
查看acf

1
2
3
df2 = df2.dropna()
# 解决有nan的问题
plot_acf(df2,lags=50).show()

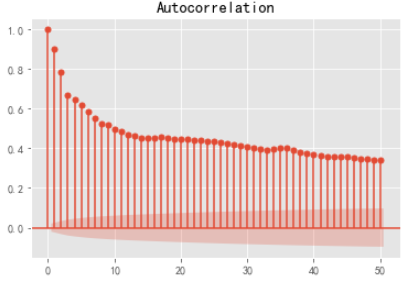
解读 拖尾为p 。基本大于0.5 现在和未来有很强的相关性

单位根检验

1
print('原始序列的ADF检验结果为：',ADF(df2.cod))

原始序列的ADF检验结果为： (-7.19465930048855, 2.452407467867345e-10, 37, 9199, {‘1%’: -3.431061069214289, ‘5%’: -2.8618542472812902, ‘10%’: -2.5669372687639176}, 11281.50483165621)

解读：P值小于显著性水平α（0.05），不接受原假设（非平稳序列），说明原始序列是平稳序列。

白噪声检验

1
print('一阶差分序列的白噪声检验结果为：',acorr_ljungbox(df2,lags=1,return_df =bool))

一阶差分序列的白噪声检验结果为： lb_stat lb_pvalue 1 7467.631465 0.0

p值为0小于0.05，不是白噪声

综上可以采用 arima 模型

定阶 人工识图

1
2
3
4
5
6
7
8
9
10
#一阶差分，我们不需要这么做，看下代码怎么写的。
df2_mn=df2.diff(periods=1, axis=0).dropna()
#自相关图
plot_acf(df2,lags=20).show()
#解读：拖尾 有长期相关性 p 取1 
#偏自相关图 
plot_pacf(df2,lags=20).show()
#偏自相关图
plot_pacf(df2,lags=50).show()
#解读：自相关图，0阶拖尾；偏自相关图，截尾。则ARIMA(p,d,q)=ARIMA(1,0,n)

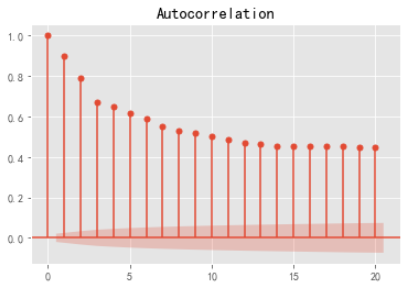
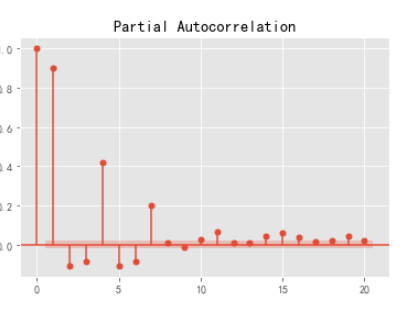
参数调优

AIC调优

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from statsmodels.tsa.arima.model import ARIMA
aic_matrix=[]
for p in range(5):
    tmp=[]
    for q in range(5):
        try:
            tmp.append(ARIMA(df2,order=(p,0,q)).fit().aic)
        except:
            tmp.append(None)
    aic_matrix.append(tmp)
aic_matrix

# p,q=aic_matrix.stack().idxmin() #最小值的索引
# 手动查找最小值 同样为1，0，4

也可以用BIC调优 不再赘述

模型建立

1
2
model = ARIMA(df2, order=(1, 0, 4))
result_arima = model.fit()

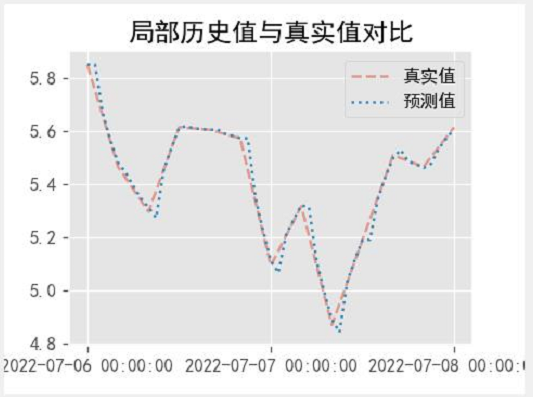
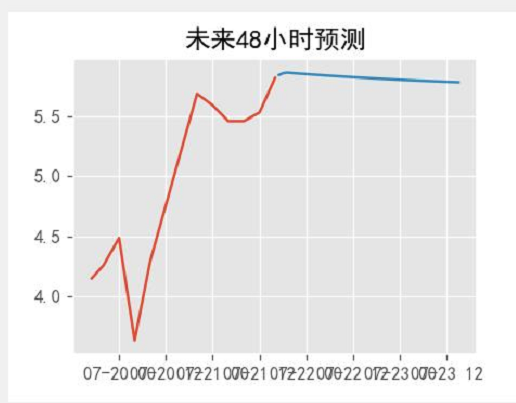
模型预测

定义画图函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def pic1(result_arima,df2):
    t1 = "2022/7/6 00:00:00"
    t2 = "2022/7/8 00:00:00"
    predict_more=result_arima.predict(t1 ,t2 )
    t = pd.date_range(t1, t2 , freq="h").strftime("%y%m%d%h%m%s")
    new_ticks = pd.date_range(t1, t2 , freq="d").strftime("%y%m%d%h%m%s")
    axc.clear()
    axc.set_title("局部历史值与真实值对比")
    axc.plot(t,df2[t1 :t2],linestyle = "--",alpha=0.5)
    axc.plot(t,predict_more,linestyle = ":")
    axc.legend(['真实值','预测值'])
    axc.set_xticks(new_ticks)   

    # 创建画布控件
    canvas = FigureCanvasTkAgg(fig1, master=root)  # A tk.DrawingArea.
    canvas.draw()
    canvas.get_tk_widget().place(x=63,y=200)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def fore_picture(result_arima,df2):
    df3 = df2.reset_index(drop=False)
    rows = df3.shape[0]
    endtime = df3.iloc[rows - 1, 0]
    forecast = pd.Series(result_arima.forecast(48), index=pd.date_range(endtime, periods=48, freq='H'))
    df_last = df2.iloc[-48:]    
    data = pd.concat((df_last, forecast), axis=0)
    data.columns = ['监测值浓度', '未来48小时']
    axc2.clear()
    axc2.set_title("未来48小时预测")
    axc2.plot(data) 
    
        # 创建画布控件
    canvas = FigureCanvasTkAgg(fig2, master=root)  # A tk.DrawingArea.
    canvas.draw()
    canvas.get_tk_widget().place(x=600,y=200)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
def compare2(result_arima,df2):
    df3 = df2.reset_index(drop=False)
    rows = df3.shape[0]
    endtime = df3.iloc[rows - 1, 0]
    starttime = df3.iloc[0, 0]
    predict=result_arima.predict(starttime , endtime)
    axc3.clear()
    axc3.set_title("全部预测值真实值对比")
    axc3.plot(df2.index,df2['cod'],linestyle = "--",alpha=0.5)
    axc3.plot(df2.index,predict,linestyle = ":")
    axc3.legend(['真实值','预测值'])
    canvas = FigureCanvasTkAgg(fig3, master=root)  # A tk.DrawingArea.
    canvas.draw()
    canvas.get_tk_widget().place(x=1200,y=200)

模型可视化及GUI初探

用Tkinter 实现自动选择站点及因子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
# 副本
from tkinter.ttk import *
from  tkinter import *
import matplotlib
matplotlib.use('TkAgg')
from matplotlib.backends.backend_tkagg import FigureCanvasTkAgg
from matplotlib.figure import Figure

root = Tk()
root.title("ARIMA预测模型")
root.geometry("1800x900+50+50")  # 长x宽+x*y
           
lb1 = Label(root,text='站点选择',fg='black', font=('微软雅黑',15),  height=2,  relief=FLAT)
lb2 = Label(root,text='因子选择',fg='black', font=('微软雅黑',15),  height=2,  relief=FLAT)
lb3 = Label(root,text='预测结果（48h）',fg='black', font=('微软雅黑',15),  height=2,  relief=FLAT)
# lb4 = Label(root,text='历史预测对比',fg='black', font=('微软雅黑',15),  height=2,  relief=FLAT)

# lb5 = Label(root,text=comb1.get(),fg='black', font=('微软雅黑',15),  height=2,  relief=FLAT)
lb1.place(x=63,y=20)
lb2.place(x=300,y=20)
lb3.place(x=63,y=110)
# lb4.place(x=510,y=110)
# lb5.place(x=820,y=110)
var1 = StringVar()
comb1= Combobox(root,textvariable=var1,values = site)
comb1.place(x=63,y=80)
var2 = StringVar()
comb2= Combobox(root,textvariable=var2,values=factor)
comb2.place(x=300,y=80)

def select_device(event):
    s = comb1.get()
    print(s)
    return s

def select_factor (event):
    y = comb2.get()
    print(y)
    return y

comb1.bind("<<ComboboxSelected>>", select_device)
comb2.bind("<<ComboboxSelected>>", select_factor)

def click(event):
    s = comb1.get()
    y = comb2.get()
    df2 = nseri(s,y )
    model = ARIMA(df2, order=(1, 0, 4))
    result_arima = model.fit()
    
    fig1 = Figure(figsize=(4, 3), dpi=120)
    axc = fig1.add_subplot(111)
    axc.clear()
    pic1(result_arima,df2)

    fig2 = Figure(figsize=(4, 3), dpi=120)
    axc2 = fig2.add_subplot(111)
    axc2.clear()
    fore_picture(result_arima,df2)

    fig3 = Figure(figsize=(4, 3), dpi=120)
    axc3 = fig3.add_subplot(111)
    axc3.clear()
    compare2(result_arima,df2)    
    

but1 = Button(root, text='计算',font=('微软雅黑',15),  height=1)
but1.place(x=300,y=110)  

but1.bind("<Button-1>",click)

root.mainloop()

结果预览
111.png

模型评价

模型评价方法： 浓度准确率， 等级准确率

浓度准确率

等级准确率：实测的类别与预测的类别相同时，则视为预测正确，预测正确的个数占预测的总个数的百分比，即为模型预测准确率。指标预测准确率的详细计算方法如下式：image.png

Pi为类别相对误差，T 为验证期内实测值的时间点数，t为实测值与预测值对应的时刻，pit为实测的类别与模拟的类别相比值，如果类别相同则为1，否则为0。

结果提取

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def format1(df2):
    df7=pd.Series()
    for i in range(180) :
        df3= df2[:-4*(1+i)]        
        model = ARIMA(df3, order=(1, 0, 4))
        result_arima1 = model.fit()
        df4 = df3.reset_index(drop=False)
        rows = df4.shape[0]
        endtime = df4.iloc[rows - 1, 0]
        forecast = pd.Series(result_arima1.forecast(5), index=pd.date_range(endtime, periods=5, freq='H'))
        df8 = forecast.tail(1)    
        df7 = pd.concat((df7,df8),axis=0,join='inner')
    return df7 
f2 =format1(df2)
f2.to_excel("forceful.xls")

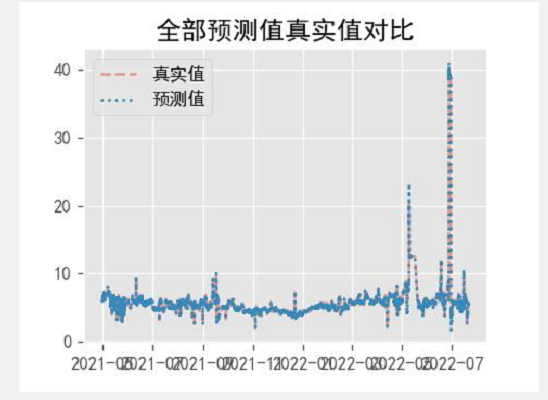
结果分析

时间原因用的excel 分析

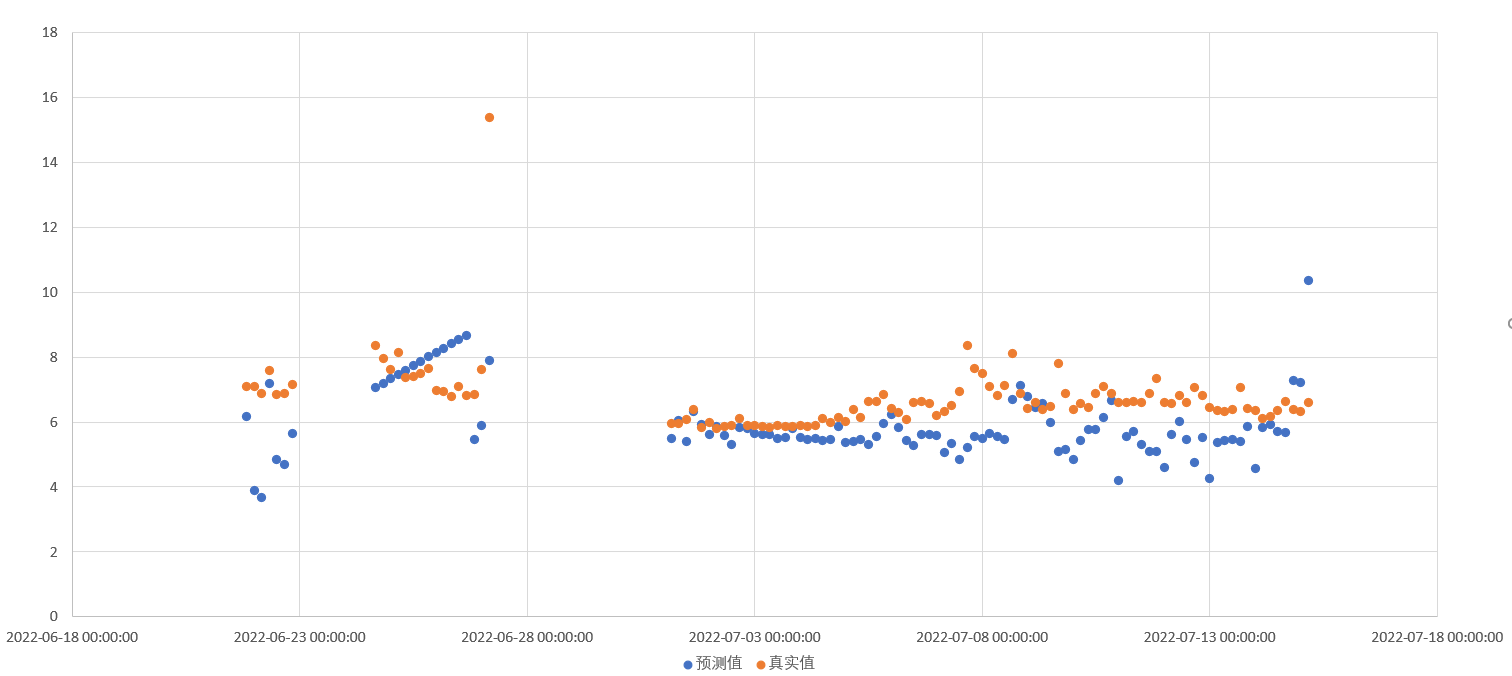
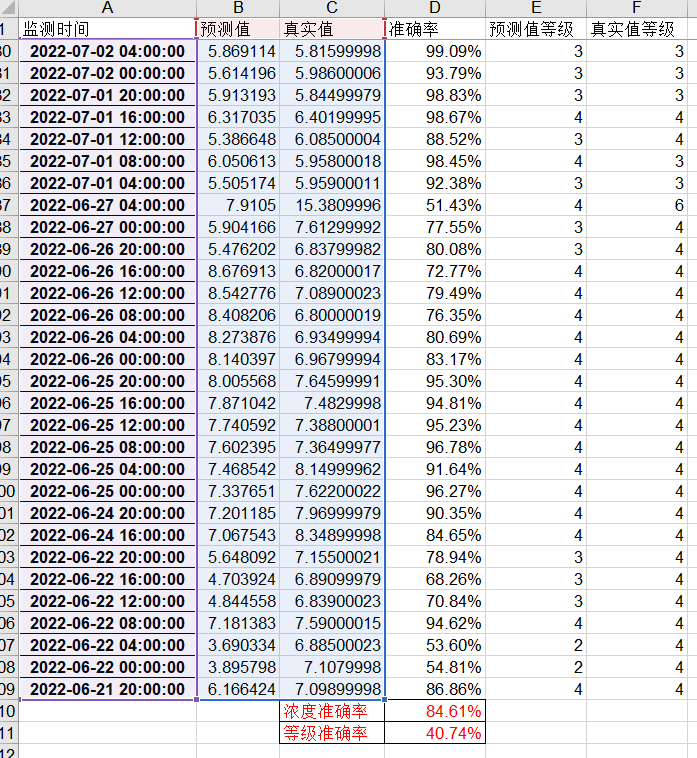
对比了6月21日~2022/7/15 高指真实值与预测值的结果，浓度预测准确率为84.61%，等级准确率40.74%，等级准确率偏低的原因为实际监测结果在6附近波动，为Ⅲ类水质标准。
预测对比时间窗口存在降雨，实际结果有一定波动，浓度预测准确率能到达84.6%，有一定的推广价值。

ARIMA .summary() 解读

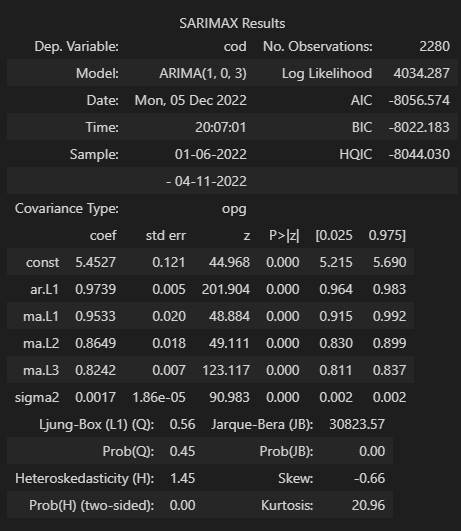
  1. 左上 为模型基本信息，Dep. Variable（需要预测的变量）、Model（模型及其参数）、Date、Time、Sample（样本数据）、No. Observations（观测数据的数量）
  2. 右上 Log Likelihood（对数似然函数）标识最适合采样数据的分布。虽然它很有用，但AIC和BIC会惩罚模型的复杂性，这有助于使我们的ARIMA模型变得简洁。赤池的信息准则（AIC）有助于确定线性回归模型的强度。AIC 会惩罚添加参数的模型，因为添加更多参数将始终增加最大似然值。贝叶斯信息准则（BIC）与 AIC 一样，BIC 也会惩罚模型的复杂性，但它也包含数据中的行数。Hannan-Quinn信息标准（HQIC），与AIC和BIC一样是模型选择的另一个标准；但是它在实践中并不常用。AIC 、BIC 越小越好
  3. 中部 确保模型中的每个项在统计意义上是否显著。若p值大于0.05，则项不显著。
  4. 下部：Ljung-Box（modified Box-Pierce test）测试错误是白噪音 Ljung-Box (L1) (Q) 为Lag1的LBQ检验统计量，其Prob(Q)为 0.01，p值为0.94。由于p值高于0.05，因此我们不能拒绝零假设（误差是白噪音）

讨论与总结

  1. ARIMA 模型在高锰酸盐指数上的预测效果超过80%,经过初步研究，适用于水质在线站点。
  2. 模型可用于单站点单因子预测，不需要其他参数，约束小，预测精度高。
  3. 模型对波动剧烈的因子，预测效果不好，不适用于所有因子，所有站点。
  4. 对于新的数据集需要做平稳性检验，白噪声检验。
  5. 需要采用数据人工识图+自动的方式实现定阶，选择最优的 p，d，q。
  6. 可以继续在 ARIMAX（多元时间序列模型）等方面深入研究。

相关文章

prophet时间序列模型水质预测应用
时间序列
#时间序列 #水环境分析 #python #用心长文
ARIMA时间序列模型水质预测应用
https://maoyu92.github.io/2024/05/09/01 时间序列/ARIMA时间序列模型水质预测应用/
作者
陈文茂
发布于
2024年5月9日
许可协议